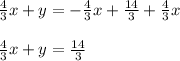Question

Write an equation in standard form for the line that passes through (5, -2) and is perpendicular to 3x-4y=12.

Answer 1

Answer:
`(4)/(3)x+y=(14)/(3)`

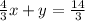
Explanation:

The Slope-Intercept form of an equation of the line is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

The equation of the line in Standard form is:

`Ax + By = C`

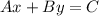
Where "A" is a positive integer, and "B" and "C" are integers.

Given the equation:

`3x-4y=12`

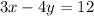
Solve for "y" in order to write it in Slope-Intercept form:

`3x-4y=12\\\\-4y=-3x+12\\\\y=(3)/(4)x-3`

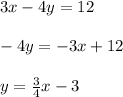
Notice that:

`m=(3)/(4)`

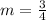
Since the slopes of perpendicular lines are negative reciprocals, the slope of the other line is:

`m=-(4)/(3)`

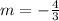
Knowing tha it passes through the point (5, -2), you can substistute the slope and the coordinates of that point into
`y=mx+b` and solve for "b":

`-2=-(4)/(3)(5)+b\\\\-2=-(20)/(3)+b\\\\-2+(20)/(3)=b\\\\b=(14)/(3)`

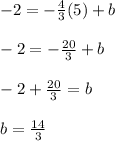
Then, the equation of this line in Slope-Intercept form is:

`y=-(4)/(3)x+(14)/(3)`

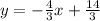
In order to write it in Standard form, add
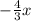`-(4)/(3)x` to both sides of the equation. Then:

`(4)/(3)x+y=-(4)/(3)x+(14)/(3)+(4)/(3)x\\\\(4)/(3)x+y=(14)/(3)`