Answer:
The exponential function to model the situation is p = 10800
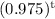
Explanation:
Given as :
The population of small town in 2002 = 10,800
The rate of decrease in population = r = 2.5%
Let The number of years of population decrease = t years
Let The population after n years = p
Now, According to question
The population after n years = The population of small town in 2002 ×
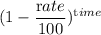
or, p = 10800 ×
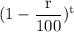
or, p = 10800 ×

or, p = 10800 ×
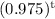
∴ p = 10800
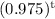
Hence, The exponential function to model the situation is p = 10800
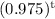 . Answer
. Answer