Explanation:
a. separate the variables
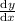 = 500-y
= 500-y
dy/(500-y) = dx
b. integrating your equation in part a to find the general equation of
differential
Integrating on both sides
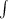 dy/(500-y) =
dy/(500-y) =
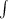 dx
dx
-㏑(500-y) = x +C ..............(1)
where C is constant of integration
c. If y(0) = 7
putting in equation (1)
-㏑(500-7) = 0+C
C = -㏑493
d. The particular solution is
-㏑(500-y) = x -㏑473
㏑473/(500-y) = x
473 = (500-y)
