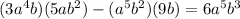Question

(3a^4b)(5ab^2)-(a^5b^2)(9b)

Answer 1

The expanded value of the given expression is

`(3a^4b)(5ab^2)-(a^5b^2)(9b)=6a^5b^3`

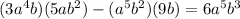
Explanation:

Given expression is

`(3a^4b)(5ab^2)-(a^5b^2)(9b)`

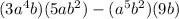
To find the value of the given expression:

`(3a^4b)(5ab^2)-(a^5b^2)(9b)=15a^5b^3-9a^5b^3`

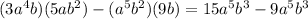
(By multiplying the products and doing algebraci subtracion of the above expression)

Now taking the common terms in the above equation we get

`(3a^4b)(5ab^2)-(a^5b^2)(9b)=3a^5b^3(5-3)`

`=3a^5b^3(2)`

`=6a^5b^3`

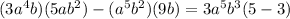
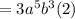
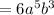
Therefore the expanded value of the given expression is

`(3a^4b)(5ab^2)-(a^5b^2)(9b)=6a^5b^3`