Question

Luke spendsA total of $41 on three drinks and 10 bags of popcorn Christopher spend a total of $11 on two drinks and two bags of popcorn right assessment equations that can be used to find the price of one using these equations determine the state the price of the bag of popcorn to the nearest cent

Answer 1

System of equations that can be used to find the price of one drink and the price of one bag of popcorn is:

3d + 10p = 41

2d + 2p = 11

Price of a bag of popcorn is $ 3.5

Solution:

Let "d" be the price of one drink

Let "p" be the price of 1 bag of popcorn

Luke spends total of $41 on three drinks and 10 bags of popcorn

3 drinks x price of one drink + 10 bags of popcorn x price of 1 bag of popcorn = 41

`3 * d + 10 * p = 41`

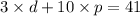
3d + 10p = 41 ------ eqn 1

Christopher spend a total of $11 on two drinks and two bags of popcorn

2 drinks x price of one drink + 2 bags of popcorn x price of 1 bag of popcorn = 11

`2 * d + 2 * p = 11`

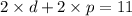
2d + 2p = 11 ------- eqn 2

Eqn 1 and eqn 2 represents system of equations that can be used to find the price of one drink and the price of one bag of popcorn

Let us solve eqn 1 and eqn 2 to find values of "d" and "p"

Multiply eqn 2 by 5

10d + 10p = 55 --- eqn 3

Subtract eqn 3 from eqn 1

3d + 10p = 41

10d + 10p = 55

(-) ------------------------

-7d = -14

d = 2

From eqn 2,

2d + 2p = 11

2(2) + 2p = 11

4 + 2p = 11

2p = 7

p = 3.5

Thus price of 1 bag of popcorn is $ 3.5 and price of one drink is $ 2