Answer:
Length of Major Axis: 6√2
Length of Minor Axis: 4√2
Explanation:
The general equation of the ellipse is:
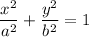 where
where
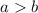 .
.
Then the major axis is along
 .
.
If the equation of the ellipse of of the form
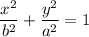 where
where
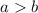 .
.
In this case, the equation of the major axis is along the
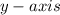 .
.
Here, the given equation of the second form.
The length of the major axis = 2a
The length of the minor axis = 2b
The given equation of the ellipse is:
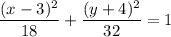
Therefore,
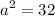 and
and
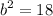 .
.
The length of the major axis = 2(√32) = 6√2
The length of the minor axis = 2(√18) = 4√2