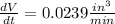Question

1. The mechanics at Lincoln Automotive are reborning a 6 in deep cylinder to fit a new piston. The machine they are using increases the cylinder’s radius one-thousandth of an inch every 3 minutes. How rapidly is the cylinder volume increasing when the bore (diameter) is 3.8 inches?

Answer 1

`0.0239(in^(3))/(min)`

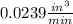
Explanation:

In order to solve this problem, we must start by drawing a diagram of the cylinder. (See attached picture)

This diagram will help us visualize the problem better.

So we start by determining what data we already know:

Height=6in

Diameter=3.8in

Radius = 1.9 in (because the radius is half the length of the diameter)

The problem also states that the radius will increase on thousandth of an inch every 3 minutes. We can find the velocity at which the radius is increasing with this data:

`r'=(1/1000in)/(3min)`

which yields:

`r'=(1)/(3000)(in)/(min)`

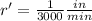
with this information we can start solving the problem.

First, the problem wants us to know how fast the volume is increasing, so in order to find that we need to start with the volume formula for a cylinder, which is:

`V=\pi r^(2)h`

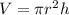
where V is the volumen, r is the radius, h is the height and π is a mathematical constant equal approximately to 3.1416.

Now, the height of the cylinder will not change at any time during the reborning, so we can directly substitute the provided height, so we get:

`V=\pi r^(2)(6)`

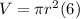
or

`V=6 \pi r^(2)`

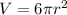
We can now take the derivative to this formula so we get:

`(dV)/(dt)=2(6)\pi r (dr)/(dt)`

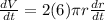
Which simplifies to:

`(dV)/(dt)=12\pi r (dr)/(dt)`

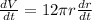
We can now substitute the data provided by the problem to get:

`(dV)/(dt)=12\pi (1.9) ((1)/(3000))`

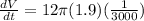
which yields:

`(dV)/(dt)=0.0239(in^(3))/(min)`