Answer:
The missing length is 2x+5
Explanation:
Given equation of volume of cuboid is V=
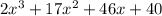
Figure show that
Length of cuboid is ?
Width of cuboid is (x+4)
Height of cuboid is (x+2)
The volume of cuboid is given by
V=Length x Width x Height
Let Length be (bx+a)
The volume of cuboid will be
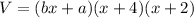
![V=(bx+a)[x^(2)+4x+2x+8 ]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/m1a0pw5sv8a3iqqt8a0v7255pjuu1tm9rv.png)
![V=bx[x^(2)+6x+8]+a[x^(2)+6x+8]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/grg655g1x0arm4etx51mhjwtalnnwyfk3v.png)
![V=[bx^(3)+6bx^(2)+8bx]+[ax^(2)+6ax+8a]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/zggo98eir6d5n2a3j8ro893mpee2lgshus.png)
![V=[bx^(3)+(6b+a)x^(2)+(8b+6a)x+8a]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/j5cr8vavfokb4ublsa4fiy6jr2yewfwa8q.png)
On comparing coefficient with given equation of volume
We get,
b=2 and 8a=40
Therefore, the value of a is 5 and b is 2
Thus, The missing length is bx+a=2x+5