Answer:
n is a positive integer and here 90, 91, 92, 93, 94 and 95 is 9⁰ = 1
9¹ = 9
9² = 81
9³ = 729
9⁴ = 6561
9⁵ = 59049
so mathematical induction is prove given below.
Explanation:
9⁰ = 1
9¹ = 9
9² = 81
9³ = 729
9⁴ = 6561
9⁵ = 59049
lets us consider by P (n) for the base case n = 0 then 9⁰ = 1 So P (1) is true
k ≥ 1so consider all integers
1≤l≤ k
There is a need to prove P (k+1)
if k is odd
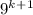 =
=
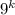 .9.
.9.
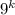 is 9 so
is 9 so
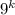 = 9 +10m
= 9 +10m
then
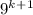 = 9 ( 9 + 10m)
= 9 ( 9 + 10m)
=81 + 10 (9m)
so digit is 1 and k +1 is even