Question

John measures the angle of depression to his house of 35 degrees and to the parade 42 degrees.If he is 3500 ft from his house how far is he from the parade to the nearest ten feet?

Answer 1

2720 ft.

Explanation:

Let John measure angle of depression to his house (at D) of 35° and to the parade (at C) 42° from a height of building AB where B is the bottom and A is the top of the building.

Now, given that BD = 3500 ft,

∠ OAD = ∠ ADB = 35° {Alternate angles}

and ∠ OAC = ∠ ACB = 42° {Alternate angles}

Now, from Δ ABD,

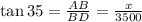`\tan 35 = (AB)/(BD) = (x)/(3500)` {Where AB = x feet.}

⇒
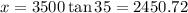`x = 3500 \tan 35 = 2450.72` ft.

Now, taking Δ ABC,

`\tan 42 = (AB)/(BC) = (x)/(BC) = (2450.72)/(BC)`

⇒
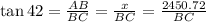
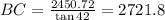`BC = (2450.72)/(\tan 42) = 2721.8` ft.

Therefore, the parade is 2720 ft far from John. (Answer)

{To the nearest ten feet}