Question

10. Working Students An education researcher claims that 57% of college

students work year-round. In a random sample of 300 college students, 171

say they work year-round. At a = 0.10, is there enough evidence to support

the researcher's claim?

Answer 1

Answer: Yes

Explanation:

As per the given information, we have to test the hypothesis:

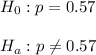`H_0:p=0.57\\\\ H_a:p\\eq0.57` , where p = Population proportion of college students work year-round.

Since the alternative hypothesis is two-tailed , so test is a two-tailed test.

In a random sample of 300 college students, 171 say they work year-round.

⇒ sample size : n= 300

⇒ sample proportion :
`\hat{p}=(171)/(300)=0.57`

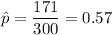
Test statistics :
`z=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}`

`z=\frac{0.57-5.57}{\sqrt{(0.57(1-0.57))/(300)}}\\\\=0`

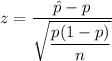
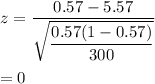
P-value = 2P(Z>|z| = 2P(Z>|0|))

=2P(Z>0) = 2(1-P(Z<0)) [∵ P(Z>z)=1-P(Z<z)]

=2(1-0.50) [ By z-table]

=1.00

Decision : P-value(1.00) > Significance level (0.10) , it means we cannot reject the null hypothesis.

We conclude that there is enough evidence to support researcher's claim that 57% of college students work year-round.