Question

A reaction is known to exhibit 1st order kinetics. At 300K the concentration of reactant is reduced to one half of its initial value after 5000s. In contrast, at 310K the conc. is halved after 1000s. Using this information to calculate:i) the rate constant for the reaction at 300Kii) the time required for the reaction to be reduced to halfiii) the activation energy for the reaction

Answer 1

The rate constant at 300 K , k = 0.0001386 s⁻¹

5000 s is the time required.

The activation energy is:- 124453.22 J/mol

Step-by-step explanation:

(i)

Half life is the time at which the concentration of the reactant reduced to half. So, 5000 s is the half life.

At 300 K

Half life expression for first order kinetic is:

Half life = 5000 s

`t_(1/2)=\frac {ln\ 2}{k}`

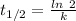
Where, k is rate constant

So,

`k=\frac {ln\ 2}{t_(1/2)}`

`k=\frac {ln\ 2}{5000}\ s^(-1)`

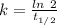
The rate constant, k = 0.0001386 s⁻¹

(ii)

As, stated above, Half life is the time at which the concentration of the reactant reduced to half. So, 5000 s is the time required.

(iii)

At 310 K , Half life = 1000 s

`k=\frac {ln\ 2}{t_(1/2)}`

`k=\frac {ln\ 2}{1000}\ s^(-1)`

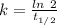
The rate constant, k = 0.0006931 s⁻¹

Using the expression,

`\ln (k_(1))/(k_(2)) =-(E_(a))/(R) \left ((1)/(T_1)-(1)/(T_2) \right )`

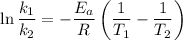
Wherem

`k_1\ is\ the\ rate\ constant\ at\ T_1`

`k_2\ is\ the\ rate\ constant\ at\ T_2`

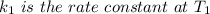
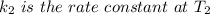
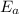`E_a` is the activation energy

R is Gas constant having value = 8.314 J / K mol

`k_2=0.0006931\ s^(-1)`

`k_1=0.0001386\ s^(-1)`

`T_1=300\ K`

`T_2=310\ K`

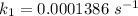
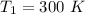
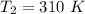
So,

`\ln (0.0001386)/(0.0006931) =-(E_(a))/(8.314) * (\left ((1)/(300)-(1)/(310) \right ))`

`-(1)/(9300)* (E_a)/(8.314)=\ln \left((0.0001386)/(0.0006931)\right)`

`-(E_a)/(77320.2)=\ln \left((0.0001386)/(0.0006931)\right)`

`E_a=-77320.2\ln \left((0.0001386)/(0.0006931)\right)\ J/mol`

`E_a=124453.22\ J/mol`

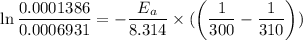
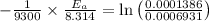
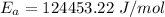
The activation energy is:- 124453.22 J/mol