Answer:
It must have 4 roots
Explanation:
Fundamental Theorem of Algebra
One polynomial of degree n will have exactly n roots. The degree of a polynomial is the highest exponent of its variable. Some of the roots could be real, some could be imaginary (complex). If n is odd, at least one of the roots is real.
The polynomial given in the question is
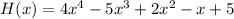
has a degree of 4 (the highest exponent of x). According to the Fundamental Theorem of Algebra, it must have 4 roots