Question

2. When Joey dives off a diving board, the equation of his pathway can be modeled by h = -16- + 15 + 12.

a) Find Joey's maximum height.
b) Find the time it will take for Joey to reach the water.
mat hinh
The rocket's height above the ground is​

Answer 1

a) The maximum height is approx 15.5 unit.

b) The time it will take for Joey to reach the water is 1.45 hour.

Explanation:

Given : When Joey dives off a diving board, the equation of his pathway can be modeled by
`h(t)= -16t^2+15t + 12`

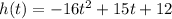
To find : a) Find Joey's maximum height.

b) Find the time it will take for Joey to reach the water.

Solution :

Modeled
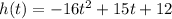`h(t)= -16t^2+15t + 12` ....(1)

a) To find maximum height

Derivate (1) w.r.t. t,

`h'= -32t+15`

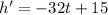
For critical point put h'=0,

`-32t+15=0`

`t=(15)/(32)`

`t=0.46875`

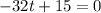
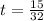
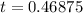
Derivate again w.r.t. t,

`h''= -32<0`

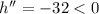
It is maximum at t=0.46875.

Substitute t in equation (1),

`h(0.46875)= -16(0.46875)^2+15(0.46875)+12`

`h(0.46875)= -3.515625+7.03125+12`

`h(0.46875)= 15.515625`

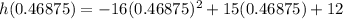
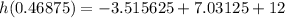
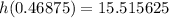
The maximum height is approx 15.5 unit.

b) To find the time it will take for Joey to reach the water.

Put h=0 in equation (1),

`-16t^2+15t + 12=0`

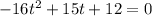
Apply quadratic formula,
`x=(-b\pm√(b^2-4ac))/(2a)`

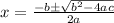
Here, a=-16 , b=15, c=12

`t=(-15\pm√((15)^2-4(-16)(12)))/(2(-16))`

`t=(-15\pm√(225+768))/(-32)`

`t=(-15\pm√(993))/(-32)`

`t=(-15+√(993))/(-32),(-15-√(993))/(-32)`

`t=−0.515,1.453`

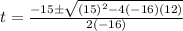
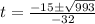
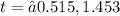
Reject negative value.

The time is t=1.45.

The time it will take for Joey to reach the water is 1.45 hour.