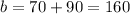Question

Bella borrowed some money from her friend in order to help buy a new video game system. Bella agreed to pay back her friend $10 per week, and after 9 weeks, Bella still owed her friend $70. Write an equation for the function

L(t), representing the amount Bella owes her friend after t weeks.

Answer 1

`L(t)=-10t+160`

Explanation:

Linear equations

Some situations can be easily modeled as a linear function. If L and t have a relation modeled by the equation of a line, then

`L(t)=mt+b`

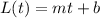
Where m is the slope or rate of change of the line, and b is the y-intercept.

Bella will pay her friend back $10 per week. It gives us how fast the payments will be done over time. The conditions of the problem tell us that when time grows, Bella will own less to her friend. That gives us a negative rate of change, i.e. m=-10

If L(t) is the amount Bella owes her friend after t weeks, we have.

`L(t)=-10t+b`

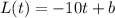
We need to determine the value of b. It will be done by using the condition stated in the question: after 9 weeks, Bella still owed her friend $70. It means that

`L(9)=70=-10(9)+b`

`b=70+90=160`

`\boxed{L(t)=-10t+160}`