Question

A researcher expects a treatment to produce an increase in the population mean. The treatment is evaluated using a one tailed hypothesis test, and the test produces z = +1.85. Based on this result, what is the correct statistical decision?

A) The researcher should reject the null hypothesis with a = .05 but not with a = .01.
B) The researcher should reject the null hypothesis with either a = .05 or a = .01.
C) The researcher should fail to reject H0 with either a = .05 or a = .01.
D) This cannot be answered without additional information.

Answer 1

A) The researcher should reject the null hypothesis with a = .05 but not with a = .01.

Explanation:

State the null and alternative hypotheses to be tested

On this case we can assume that the researcher conduct a one right tailed test hypothesis like on this way:

Null hypothesis:
`\mu \leq \mu_o`

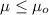
Alternative hypothesis:
`\mu > \mu_o`

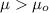
The statistic for this case is given by:

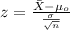`z=(\bar X-\mu_o)/((\sigma)/(√(n)))` (1)

z-test: "Is used to compare group means. Is one of the most common tests and is used to determine if the mean is (higher, less or not equal) to an specified value".

On this case we have the value for z score given z =+1.85

It's important to refresh the p value method or p value approach . "This method is about determining "likely" or "unlikely" by determining the probability assuming the null hypothesis were true of observing a more extreme test statistic in the direction of the alternative hypothesis than the one observed". Or in other words is just a method to have an statistical decision to fail to reject or reject the null hypothesis.

The significance level provided
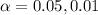`\alpha=0.05,0.01`. The next step would be calculate the p value for this test.

Since is a one right tail test the p value would be:

`p_v =P(z>1.85)=1-P(Z<1.85)=1-0.968=0.032`

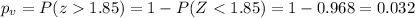
If we compare the p value obtained and the significance level given
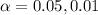`\alpha=0.05,0.01` we can take a decision:

A) The researcher should reject the null hypothesis with a = .05 but not with a = .01.

YES, since the p value it's higher than the significance level of 0.01 so we FAIL to reject the null hypothesis at this significance level. And for the significance level 0.05 we have that
`p_v <\alpha` and we can reject the null hypothesis.

B) The researcher should reject the null hypothesis with either a = .05 or a = .01.

No since the p value it's higher than the significance level of 0.01 so we FAIL to reject the null hypothesis at this significance level

C) The researcher should fail to reject H0 with either a = .05 or a = .01.

No, for the significance level of 0.05 we reject the null hypothesis since
`p_v<\alpha`

D) This cannot be answered without additional information.

No, we have enough info to answer the question