Question

The safe load, L, of a wooden beam supported at both ends varies jointly as the width, w, the square of the depth,d, and inversely as the length, l. A wooden beam 6in. wide, 9in. deep, and 12ft long holds up 1090lb. What load would a beam 5in. wide, 4in. deep and 17ft long of the same material support? (Round off your answer to the nearest pound.)

Answer 1

Safe Load is 127 lb.

Explanation:

Given:

Load (L) = 1090 lb.

width(w) = 6 in.

depth (d) = 9 in.

length (l) = 12 ft.

Since all other units are in inches and unit of length is in feet, So we will convert foot into inches we get;

1 feet = 12 inches

12 feet =
`12*12 =144 in.`

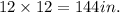
Hence length(l)= 144 in.

Now also Given

Load varies directly with width and square of depth and inversely with length.

Hence we can say that;

L∝
`(wd^2)/(l)`

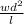
Hence
`L=(kwd^2)/(l)` where k is constant.

Now Substituting the given values we will find the value of k we get;

`1090=(k*6*9^2)/(144)\\\\1090=(k*6*81)/(144)\\\\1090*144= 486k\\\\k=(1090*144)/(486)\approx 322.96`

Also Given:

width(w) = 5 in.

depth(d) = 4 in.

length(l) = 17 ft.

1 ft. = 12 in.

17 ft =
`12 * 17 = 204\ in.`

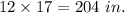
Hence length(l) = 204 in.

k = 322.96

We need to find the load beam(L);

`L=(kwd^2)/(l)`

Substituting new values we get;

`L = (322.96* 5* 4^2)/(204) = (322.96* 5* 16)/(204) = 126.65\ lb`

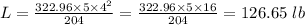
Rounding the load in nearest pound we get;

Load beam(L) = 127 lb

Hence Safe Load is 127 lb.