Question

8–6. Determine the maximum force P that can be exerted on each of the two pistons so that the circumferential stress in the cylinder does not exceed 3 MPa. Each piston has a radius of 45 mm and the cylinder has a wall thickness of 2 mm.

Answer 1

The maximum force is 846.11 N.

Step-by-step explanation:

Given that,

Stress = 3 MPa

Radius = 45 mm

Thickness = 2 mm

We need to calculate the internal pressure

Using formula of internal pressure

`\sigma=(p* r)/(t)`

`p=(\sigma t)/(r)`

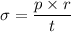
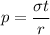
Put the value into the formula

`p=(3*10^(6)*2*10^(-3))/(45*10^(-3))`

`p=0.133*10^(6)\ Pa`

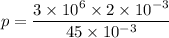
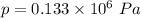
We need to calculate the maximum force

Using formula of maximum force

`p=(P)/(A)`

`P=p* A`

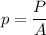
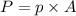
Here, P = force

p = internal pressure

Put the value into the formula

`F=0.133*10^(6)*\pi*(45*10^(-3))^2`

`F=846.11\ N`

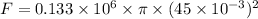
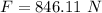
Hence, The maximum force is 846.11 N.

Answer 2

`P=2.66\ N` is the maximum safe load.

Step-by-step explanation:

Given:

• diameter of the cylinder,
  `d= 90\ mm`

• thickness of the cylinder wall,
  `t=2\ mm`

• maximum bearable stress,
  `\sigma=3\ MPa`

Firstly we find that:

`(t)/(d) =(1)/(45) <(1)/(20)`

⇒ This is a thin cylinder.

We know axial stress and hoop stress is given by

`\sigma_a=(P.d)/(4t)`

`\sigma_h=(P.d)/(2t)`

⇒ Axial load will always be larger than the circumferential load under while other parameters are same.

So we find the load in case of axial stress:

`30=(P* 90)/(4* 2)`

`P=2.66\ N` is the maximum safe load.