Question

A 1000 kg car is rolling slowly across a level surface at 1m/s, heading toward a group of small innocent children.

The doors are locked, so you can't get inside to use the brakes.

Instead, you run in front of the car and push on the hood at an angle of 30° below horizontal.


How hard must you push to stop the car in a distance of 2 m?

Answer 1

Force, F = 288.67 N

Step-by-step explanation:

Mass of the car, m = 1000 kg

Initial speed of the car, u = 1 m/s

The car and push on the hood at an angle of 30° below horizontal,
`\theta=30^(\circ)`

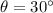
Distance, d = 2 m

Let F is the force must you push to stop the car. using work energy theorem to find it. According to this theorem, the work done is equal to the change in kinetic energy as :

`W=(1)/(2)m(v^2-u^2)`

`F* d=(1)/(2)m(v^2-u^2)`

It stops, v = 0

`Fd\ cos\theta=(1)/(2)m(u^2)`

`F=((1)/(2)m(u^2))/(d\ cos\theta)`

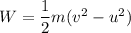
`F=((1)/(2)* 1000* (1)^2)/(2\ cos(30))`

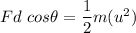
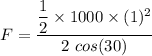
F = -288.67 N

So, the force required to push to stop the car is 288.67 N. Hence, this is the required solution.

Answer 2

The force is -1620.73 N.

Step-by-step explanation:

Given that,

Mass of car = 1000 kg

Velocity = 1 m/s

Distance = 2 m

Angle = 30°

We need to calculate the force

Using formula of work done

`W_(net)=K_(f)-K_(i)`

`F* d=K_(f)-K_(i)`

`Fd\cos\theta=-K_(i)`

`F=(-K_(f))/(d\cos\theta)`

`F=-((1)/(2)mv^2)/(d\cos\theta)`

Put the value into the formula

`F=-((1)/(2)*1000*(1)^2)/(2*\cos30)`

`F=-1620.73\ N`

Hence, The force is -1620.73 N.