Question

PLEASE HURRY!

Point Z is the incenter of triangle RST.


Point Z is the incenter of triangle S R T. Lines are drawn from the points of the triangle to point Z. Lines are drawn from point Z to the sides of the triangle to form right angles and line segments Z A, Z B, and Z C. Angle A S Z is (5 x minus 9) degrees and angle Z S B is 16 degrees.

What is the value of x?


a. x = 2

b. x = 3

c. x = 5

Answer 1

X=5, C

Explanation:

Answer 2

Option C. x = 5

Explanation:

To solve this question we should always keep these two points in our mind.

1). In-center of a triangle is formed by the intersection of the angle bisectors of all interior angles of the triangle.

2). In-center of a triangle is equidistant from all three sides of the triangle.

From the figure attached,

In ΔSRT,

∠ASZ ≅ ∠ZSB [ SZ is an angle bisector of angle ASB]

5x - 9 = 16 [ given in the question]

5x = 16 + 9

5x = 25

x =
`(25)/(5)`

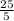
x = 5

Therefore, Option C. is the answer.