Question

A ball is launched upward from a height 40 feet above ground level. The ball’s height at t seconds is given by . (SLO #1, 6) At what time(s) will the ball be at 100 feet? Show your work. Round answer(s) to nearest tenth. In your own words, explain what was happening with the flight of the ball at the time(s) that it was at 100 feet.

Answer 1

At time t = 0.5 and t = 7.5 seconds, ball will be at the height h = 100 feet.

Explanation:

The given question is incomplete. Here is the complete question.

" A ball is launched upward form a height 40 feet above the ground level.

The ball's height at t seconds is given by h(t) = -16t² + 128t + 40.

a). At what time(s) will the ball be at 100 feet? Show your work. Round answer(s) to nearest tenth.

b). In your words, explain what was happening with the flight of the ball at the time(s) that it was at 100 feet.

a). At the height h = 100 feet

Equation will be, 100 = -16t² + 128t + 40

-16t² + 128t + 40 - 100 = 0

-16t² + 128t - 60 = 0

16t² - 128t + 60 = 0

4t² - 32t + 15 = 0

From the quadratic formula,

`t=\frac{32\pm \sqrt{(32)^(2)-4(4)(15)}}{2* 4}`

`t=(32\pm √(1024-240))/(8)`

`t=(32\pm √(784))/(8)`

`t=(32\pm 28)/(8)`

`t=(4)/(8), (60)/(8)`

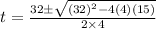
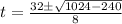
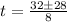
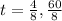
t = 0.5 sec, 7.5 seconds

b). These timings show that the ball will be at the same height of 100 feet, at t = 0.5 seconds while going upwards and at t = 7.5 while descending downwards.