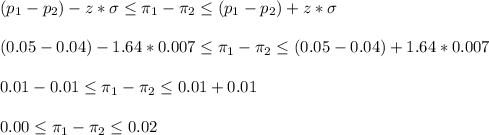Question

A certain change in a process for manufacture of component parts is being considered. Samples are taken using both the existing and the new procedure so as to determine if the new process results in an improvement. If 75 of 1500 items from the existing procedure were found to be defective and 80 of 2000 items from the new procedure were found to be defective, find a 90% confidence interval for the true difference in the fraction of defective items between the existing and new process.

Answer 1

a) The confidence interval is
`0.00\leq\pi_1-\pi_2\leq0.02`.

Explanation:

We have to calculate a confidence interval (CI) of a difference of proportions.

For the existing procedure, the proportion is:

`p_1=75/1500=0.05`

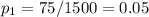
For the new procedure, the proportion is:

`p_2=80/2000=0.04`

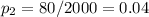
To calculate the CI, we need to estimate the standard deviation

`s=\sqrt{(p_1(1-p_1))/(n_1) +(p_2(1-p_2))/(n_2) }\\\\s=\sqrt{(0.05(1-0.05))/(1500) +(0.04(1-0.04))/(2000) }=√( 0.000032 + 0.000019 )=√(  0.000051 )\\\\s=0.007`

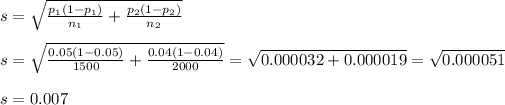
For a 90% CI, the z-value is 1.64.

Then, the CI is:

`(p_1-p_2)-z*\sigma \leq\pi_1-\pi_2\leq(p_1-p_2)+z*\sigma \\\\(0.05-0.04)-1.64*0.007\leq\pi_1-\pi_2\leq(0.05-0.04)+1.64*0.007\\\\0.01-0.01\leq\pi_1-\pi_2\leq0.01+0.01\\\\0.00\leq\pi_1-\pi_2\leq0.02`