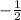Answer:
Slope =
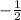
Explanation:
Slope =
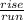
The rise in this example can be found by looking at the y-axis. We see that the line intersects the y-axis at y = 2. This is our rise.
The run can be found by looking at the x-axis. In this example, we can find the run by looking at where the line intersects with the x-axis. We see here that this interception occurs at x = 4.
So our rise is 2 and our run is 4.
Slope =
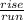
Slope =
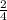
We can simplify this equation down:
Slope =

However, since the line is descending as you follow it from left to right, this makes the slope negative. If the line was ascending as it went from left to right, the slope would be positive. However, since it descends, the slope will be negative.
Slope =