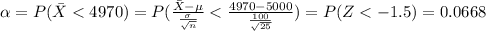Question

A new curing process developed for a certain type of cement results in a mean compressive strength of 5000 kilograms per square centimeter with a standard deviation of 100 kilograms. To test the hypothesis that µ = 5000 against the alternative that µ < 5000, a random sample of 25 pieces of cement is tested. The critical region is defined to be x<4970. Find the probability of committing a type I error when H0 is true.

Answer 1

The probability of committing a Type I error in this scenario, where the null hypothesis is true and the critical region is defined as x < 4970 with a known standard deviation and sample size, is approximately 0.0668 or 6.68%.

Step-by-step explanation:

The question is asking about the probability of committing a Type I error in the context of hypothesis testing in statistics. A Type I error occurs when the null hypothesis, H0 (that the mean compressive strength of the cement is 5000 kilograms per square centimeter), is true but is incorrectly rejected in favor of the alternative hypothesis, Ha (that the mean compressive strength is less than 5000 kilograms per square centimeter).

To find this probability, we need to calculate the significance level (α), which is the probability of obtaining a sample mean in the critical region when the null hypothesis is true. When the null hypothesis is true, we know the population mean (μ) is 5000, and we are given the population standard deviation (σ) is 100 and the sample size (n) is 25. We use this information to calculate the z-score corresponding to the sample mean in the critical region, x = 4970:

Z = (x - μ) / (σ / √ n) = (4970 - 5000) / (100 / √ 25) = -30 / (100 / 5) = -30 / 20 = -1.5

The probability corresponding to a z-score of -1.5 can be found using a standard normal distribution table or a statistical software tool. This value gives us the probability of committing a Type I error or the significance level (α). In this example, looking up a z-score of -1.5 in a standard normal table typically gives a value around 0.0668.

Therefore, the probability of committing a Type I error when H0 is true, is approximately 0.0668 or 6.68%.

Answer 2

`\alpha =0.0668`

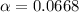
Step-by-step explanation:

Data given and notation

The info given by the problem is:

`n=25` the random sample taken

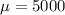`\mu =5000` represent the population mean

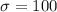`\sigma =100` represent the population standard deviation

The critical region on this case is
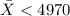`\bar X <4970` so then if the value of
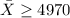`\bar X \geq 4970` we fail to reject the null hypothesis. In other case we reject the null hypothesis

Null and alternative hypotheses to be tested

We need to conduct a hypothesis in order to determine if the true mean is 5000, the system of hypothesis would be:

Null hypothesis:
`\mu = 5000`

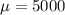
Alternative hypothesis:
`\mu \\eq 5000`

Let's define the random variable X ="The compressive strength".

We know from the Central Limit Theorem that the distribution for the sample mean is given by:

`\bar X \sim N(\mu , (\sigma)/(√(n)))`

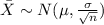
Find the probability of committing a type I error when H0 is true.

The definition for type of error I is reject the null hypothesis when actually is true, and is defined as
`\alpha` the significance level.

So we can define
`\alpha` like this:

`\alpha= P(Error I)= P(\bar X <4970, when,\mu = 5000)`

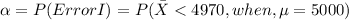
And in order to find this probability we can use the Z score given by this formula:

`Z=(\bar X -\mu)/((\sigma)/(√(n)))`

And the value for the probability of error I is givn by:

`\alpha= P(\bar X <4970) =P((\bar X -\mu)/((\sigma)/(√(n)))<(4970 -5000)/((100)/(√(25))))=P(Z<-1.5)=0.0668`