Question

Line Segment BC has endpoints B (3,5) and C (7,15). Find the missing coordinates of A (x,9) and D (17,y) such that AB and CD are perpendicular to BC.

Answer 1

x=-7

y=11

Explanation:

Perpendicular Vectors

Two vectors defined as their endpoints
`\vec u=<a,b>` and
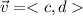`\vec v=<c,d>` are perpendicular if their dot product a.b is zero. The dot product is

`\vec u.\vec v=ac+bd`

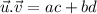
In other words

ac+bd=0

Let's treat all the points as the extremes of vectors, so we can easily find the missing coordinates

B (3,5) and C (7,15) define a segment, the vector

`\overrightarrow{BC}=<7-3,15-5>=<4,10>`

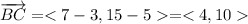
The point A is A (x,9), we need to form a vector with B

`\overrightarrow{AB}=<x-3,9-5>=<x-3,4>`

this vector must be perpendicular to BC, so, applying the dot product we have

`4(x-3)+40=0`

`4x-12=-40`

`x=-7`

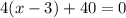
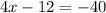
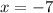
The point D is D(17,y), we need to form a vector with C

`\overrightarrow{CD}=<17-7,y-15>=<10,y-15>`

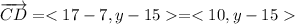
this vector must be perpendicular to BC, so, applying the dot product we have

`(4)(10)+(10)(y-15)=0`

`40+10y-150=0`

`10y=110`

`y=11`

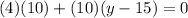
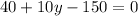
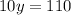
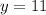
The points are

`\boxed{A(-7,9), D(17,11)}`