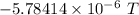Question

A plane monchromatic radio wave (lambda = 0.3 m) travels in vacuum along the positive x-axis, with an intensity I = 45 W/m2. Suppose at time t = 0, the electric field at the origin is measured to be directed along with positive y-axis with an amplitude equal to its maximum possible value. What is Bz, the magnetic field at the origin, at time t = 1.5 ns?

Answer 1

`-5.78414* 10^(-6)\ T`

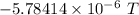
Step-by-step explanation:

`\epsilon_0` = Permittivity of free space =
`8.85* 10^(-12)\ F/m`

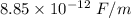
c = Speed of light =
`3* 10^8\ m/s`

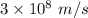
`\lambda` = Wavelength = 0.3 m

T = Time period

f = Frequency

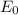`E_0` = Electric field

Intensity of electric field is given by

`I=(1)/(2)c\epsilon_0E_0^2\\\Rightarrow E_0=\sqrt{(2I)/(c\epsilon_0)}\\\Rightarrow E_0=\sqrt{(2* 45)/(3* 10^(8)* 8.85* 10^(-12))}\\\Rightarrow E_0=184.11492\ N/C`

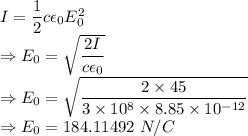
Magnetic field is given by

`B_0=(E_0)/(c)\\\Rightarrow B_0=(184.11492)/(3* 10^8)\\\Rightarrow B_0=6.13716* 10^(-7)\ T`

`k=(2\pi)/(\lambda)\\\Rightarrow k=(2\pi)/(0.3)\\\Rightarrow k=20.94\ /m`

`f=(c)/(\lambda)\\\Rightarrow f=(3* 10^(8))/(0.3)\\\Rightarrow f=1* 10^(9)\ Hz`

`T=(1)/(f)\\\Rightarrow T=10^(-9)`

`\omega=(2\pi)/(T)\\\Rightarrow \omega=(2\pi)/(10^(-9))\\\Rightarrow \omega=6283185307.17958\ rad/s`

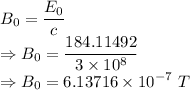
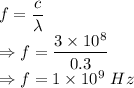
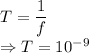
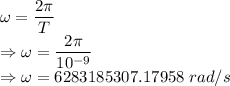
Magnetic field in the z direction is given by (x=0)

`B_z=B_0(kx-\omega t)\\\Rightarrow B_z=6.13716* 10^(-7)* (0-6283185307.17958* 1.5* 10^(-9))\\\Rightarrow B_z=-5.78414* 10^(-6)\ T`

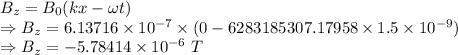
The magnetic field at the origin is
`-5.78414* 10^(-6)\ T`