Question

A port inspector working for a trading company needs to decide whether to accept a large shipment of products of a certain foreign country. He will decline the shipment if there is compelling evidence that the proportion of the defective products is more than 5 percent (0.05). Suppose that a random sample of 1000 products from this shipment has yielded At the 5 % level of significance, what decision should the port inspector make?

A) reject the null hypothesis; reject the shipment

B) reject the null hypothesis; accept the shipment

C) fail to reject the null hypothesis; accept the shipment

D) fail to reject the null hypothesis; reject the shipment

Answer 1

Option C: fail to reject the null hypothesis; accept the shipment.

Explanation:

The question is incomplete. It should say:

"A port inspector working for a trading company needs to decide whether to accept a large shipment of products of a certain foreign country. He will decline the shipment if there is compelling evidence that the proportion of the defective products is more than 5 percent (0.05). Suppose that a random sample of 1000 products from this shipment has yielded p=0.06. At the 5 % level of significance, what decision should the port inspector make?

A) reject the null hypothesis; reject the shipment

B) reject the null hypothesis; accept the shipment

C) fail to reject the null hypothesis; accept the shipment

D) fail to reject the null hypothesis; reject the shipment"

We have to perform an hypothesis test on proportion, with a sginificance level of 0.05.

The null and alternative hypothesis are:

`H_0: \pi\leq0.05\\\\H_1:\pi > 0.05`

The standard deviation is

`\sigma=\sqrt{(p(1-p))/(n) }= \sqrt{(0.05(1-0.05))/(1000) }=0.007`

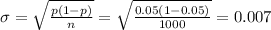
Now we can calculate the z value:

`z=(p-\pi-0.5/n)/(\sigma)=(0.06-0.05-0.5/1000)/(0.007)=(0.0095)/(0.007) =1.357`

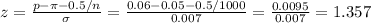
For a one-side test with z=1.357, the P-value is 0.08739.

The P-value is greater than the significance level, so the null hypothesis can not be rejected.

The inspector has no compelling evidence that the proportion of defective products is more than 5%, so he has to accept the shipment.