Answer:
Rope dancer is 2.66 meters above the ground.
Explanation:
In the figure attached,
Rope AB of length 20 meters has been tied between the poles A and B of height 9 meters.
When rope dancer is at point C, rope made 30° and 60° angles with the horizontal line AB.
Now we have to find the vertical distance of the rope dancer from the ground.
From ΔACD,
sin 30° =
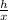
h =
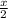
x = 2h
Similarly from ΔBCD,
sin 60° =
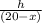
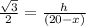
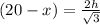
x =
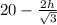
Now by equating the values of x,
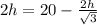
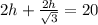
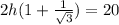
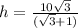
h = 6.34 m
Now (9 - h) = 9 - 6.34
= 2.66 m
Therefore, rope dancer is 2.66 meters above the ground.