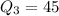Question

A sociologist records the annual household income (in thousands of dollars) among a sample of families living in a high-crime neighborhood. Locate the lower, median, and upper quartiles for the times listed below. Hint: First arrange the data in numerical order. lower quartile ____ thousand dollarsmedian ______ thousand dollars upper quartile ______ thousand dollars33 55 39 44 34 48 25 39 23 45

Answer 1

The lower quartile is
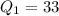`Q_1=33` thousand dollars.

The median quartile is
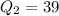`Q_2=39` thousand dollars.

The upper quartile is
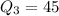`Q_3=45` thousand dollars.

Explanation:

The lower quartile is the median value of the lower half of a data set at the 25th percentile of a distribution.

The median quartile is the median value of a data set at the 50th percentile of a distribution.

The upper quartile is the median value of the upper half of a data set at the 75th percentile of a distribution.

To locate each quartile in a data set, we follow four steps:

Step 1: Put the numbers in order: 23, 25, 33, 34, 39, 39, 44, 45, 48, 55

Step 2: The median is given by
`(n+1)/(2)` where n is all scores in the data set.

Because n = 10, the median position is
`(10+1)/(2)=5.5`

The median is the average of the fifth and sixth positioned scores

`Q_2=(39+39)/(2) =39`

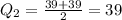
Step 3: Compute
`(n+1)/(2)` where n is all scores below
`Q_2`.

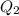For scores below
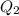`Q_2`, use only 23, 25, 33, 34, 39.

Because n = 5, the median position is
`(5+1)/(2)=3`

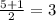
The median is the third positioned score:
`Q_1=33`

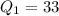
Step 4: Compute
`(n+1)/(2)` where n is all scores above
`Q_2`.

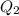For scores above
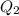`Q_2`, use only 39, 44, 45, 48, 55

Because n = 5, the median position is
`(5+1)/(2)=3`

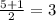
The median is the third positioned score:
`Q_3=45`