Question

Find the length of QP given Q is the midpoint of XF, PQ =2X+1, XF=7X-4, PF=X

Answer 1

Therefore the length of QP = 3.4 units

Explanation:

Given:

PQ = 2x + 1

XF = 7x - 4

PF = x

Q is the mid poimt of XF

∴ XQ = QF

QF = PQ - PF ..........( Q - F - P )

= 2x + 1 - x

∴ QF = x + 1

∴ XQ = QF = x + 1

TO Find:

QP = ?

Solution:

By Addition Property we have

`XP = XQ + QF+PF ..........(X-Q-F-P)\\\\`

`XF + PF =XQ + QF+PF ..........(X-Q-F-P)\\`

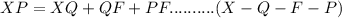
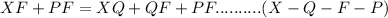
Substituting the given values in above equation we get

(7x - 4) + x = (x +1) + (x +1) + x

8x -4 = 3x +2

8x - 3x + 4 + 2

5x = 6

∴
`x = (6)/(5)`

Now we require

QP = (2x + 1)

∴
`QP = 2* (6)/(5) +1\\\\QP = (12+5)/(5) \\\\QP =(17)/(5) \\\\\therefore QP = 3.4\ unit`

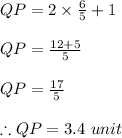
Therefore the length of QP = 3.4 units