Question

What is the length of the arc if: 11. r=10 n=20 A15(pi)/ 7 B13(pi)/ 5 C16(pi)/ 2 D11(pi)/ 4 E 10(pi)/ 9 F 9(pi)/ 4 12. r=3 n=6 Api/9 Bpi/12 Cpi/26 Dpi/10 E pi/8 F pi/4 13. r=4 n=7 A8(pi)/55 B 6(pi)/12 C7(pi)/45 D2(pi)/22 E 9(pi)/18 F 7(pi)/37 14. r=2 n=x Ax(pi)/15 Bx(pi)/30 Cx(pi)/60 Dx(pi)/90 E x(pi)/120 F x(pi)/150 15. r=y n=x A x*y*pi/90 Bx*y*pi/30 Cx*y*pi/45 Dx*y*pi/27 E x*y*pi/180 F x*y*pi/115

Answer 1

Explanation:

The formula for arc length [for the angle in degrees] is:

`L = 2\pi r \left((n)/(360)\right)`

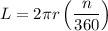
here,

`n` = degrees

`r` = radius

using this we'll solve all the parts:

r = 10, n = 20:

`L = 2\pi r \left((n)/(360)\right)`

`L = 2\pi (10) \left((20)/(360)\right)`

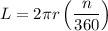
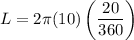
from here, it is just simplification:

2 and 360 can be resolved: 360 divided by 2 = 180

`L = \pi (10) \left((20)/(180)\right)`

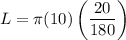
10 and 180 can be resolved: 180 divided by 10 = 18

`L = \pi \left((20)/(18)\right)`

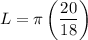
finally, both 20 and 18 are multiples of 2 and can be resolved:

`L = \pi \left((10)/(9)\right)`

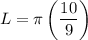
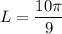`L = (10\pi)/(9)` Option (E)

r=3, n=6:

`L = 2\pi r \left((n)/(360)\right)`

`L = 2\pi (3) \left((6)/(360)\right)`

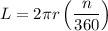
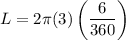
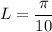`L = (\pi)/(10)` Option (D)

r=4 n=7

`L = 2\pi r \left((n)/(360)\right)`

`L = 2\pi (4) \left((7)/(360)\right)`

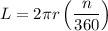
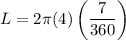
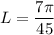`L = (7\pi)/(45)` Option (C)

r=2 n=x

`L = 2\pi r \left((n)/(360)\right)`

`L = 2\pi (2) \left((x)/(360)\right)`

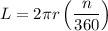
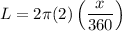
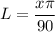`L = (x\pi)/(90)` Option (D)

r=y n=x

`L = 2\pi r \left((n)/(360)\right)`

`L = 2\pi (y) \left((x)/(360)\right)`

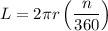
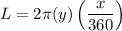
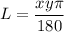`L = (xy\pi)/(180)` Option (E)