Answer:
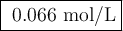
Step-by-step explanation:
We are given the amounts of two reactants, so this is a limiting reactant problem.
1. Assemble all the data in one place, with molar masses above the formulas and other information below them.
Mᵣ: 58.44
NaCl + AgNO₃ ⟶ NaNO₃ + AgCl
m/g: 0.245
V/mL: 50.
c/mmol·mL⁻¹: 0.0180
2. Calculate the moles of each reactant
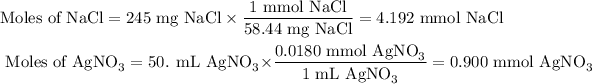
3. Identify the limiting reactant
Calculate the moles of AgCl we can obtain from each reactant.
From NaCl:
The molar ratio of NaCl to AgCl is 1:1.

From AgNO₃:
The molar ratio of AgNO₃ to AgCl is 1:1.
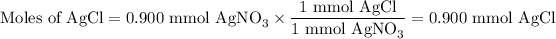
AgNO₃ is the limiting reactant because it gives the smaller amount of AgCl.
4. Calculate the moles of excess reactant
Ag⁺(aq) + Cl⁻(aq) ⟶ AgCl(s)
I/mmol: 0.900 4.192 0
C/mmol: -0.900 -0.900 +0.900
E/mmol: 0 3.292 0.900
So, we end up with 50. mL of a solution containing 3.292 mmol of Cl⁻.
5. Calculate the concentration of Cl⁻
![\text{[Cl$^(-)$] } = \frac{\text{3.292 mmol}}{\text{50. mL}} = \textbf{0.066 mol/L}\\\text{The concentration of chloride ion is $\large \boxed{\textbf{0.066 mol/L}}$}](https://img.qammunity.org/2020/formulas/chemistry/middle-school/hnwqzap1ctxhul2v5buhf6etxnihxq75rs.png)