Question

Calculate the average bond energy of the sulfur-oxygen bonds in SO2 (in kJ/mol), given the following information. SF4(g) + 2 H2O(g) → SO2(g) + 4 HF(g) ΔH = –123 kJ Bond dissociation energies: S–F 327 kJ/mol F–F 154 kJ/mol H–F 565 kJ/mol H–O 467 kJ/mol

Answer 1

520 kJ·mol⁻¹

Step-by-step explanation:

You calculate the energy required to break all the bonds in the reactants. Then you subtract the energy to break all the bonds in the products.

SF₄(g) + 2H₂O(g) ⟶ SO₂(g) + 4HF(g); ΔH = –123 kJ

Bonds: 4S-F + 4O-H 2S=O 4H-F

D/kJ·mol⁻¹: 327 467 x 565

The formula relating ΔᵣH and bond dissociation energies (D) is

`\Delta _{\text{r}}H = \sum{D_{\text{reactants}} - \sum{D_{\text{products}}`

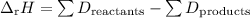
(Note: This is an exception to the rule. All other thermochemical reactions are “products – reactants”. With bond energies, it’s “reactants – products”. The reason comes from the way we define bond energies.)

Σ(Dreactants) = 4 × 327 + 4 × 467 = 3176 kJ

Σ(Dproducts) = 2x +4 × 565 = (2x + 2260) kJ

-123 =3176 - (2x + 2260)

-123 = 3176 - 2x - 2260

-123 = 916 - 2x

2x = 1039

x = 520 kJ·mol⁻¹

The average bond energy of the S=O bonds in SO₂ is 520 kJ/mol.

Answer 2

The average bond energy of the sulfur-oxygen bonds in sulfur dioxide is 519.5 kJ/mol.

Step-by-step explanation:

`SF_4(g) + 2 H_2O(g)\rightarrow SO_2(g) + 4 HF(g) ,`ΔH = -123 kJ

We are given with:

`\Delta H_(S-F)=327 kJ/mol`

`\Delta H_(H-F)=565 kJ/mol`

`\Delta H_(H-O)=467 kJ/mol`

`\Delta H_(F-F)=154 kJ/mol`

`\Delta H_(S-O)=?`

ΔH =

(Energies required to break bonds on reactant side) - (Energies released on formation of bonds on product side)

`\Delta H=(1 mol* 4* \Delta H_(S-F)+2 mol* 2* \Delta H_(H-O))-(1 mol* 2* \Delta H_(S-O)+4 mol* 1*\Delta H_(H-F))`

`\Delta H=(1 mol* 4* 327 kJ/mol+2 mol* 2* 467 kJ/mol)-(1mol* 2* \Delta H_(S-O)+4 mol* 1* 565 kJ/mol)`

`-123 kJ=(1308 kJ+1868kJ)-(1mol* 2* \Delta H_(S-O)+2260 kJ)`

`1mol* 2* \Delta H_(S-O)=123 kJ+1308 kJ+1868kJ-2260 kJ`

`\Delta H_(S-O)=(1039 kJ)/(2* 1 mol)=519.5 kJ/mol`

The average bond energy of the sulfur-oxygen bonds in sulfur dioxide is 519.5 kJ/mol.