Question

Suppose any one round of a gambling game pays 3 to 1 and the odds are 4 to 1 against you.

If you play for 100 rounds and bet one dollar on each round, what is the chance you will come out ahead?

Answer 1

There is a 10.5% chance of having a positive payoff.

Explanation:

The odds are 4 to 1 against, so we can estimate the probability of success (p) as

`(p)/(q)=(p)/(1-p)=(1)/(4)\\\\4p=1-p\\\\5p=1\\\\p=0.2`

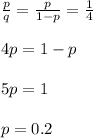
The expected pay for every success is 3 to 1, so we lose $1 for every lose and we gain $3 for every win.

The number of winnings in the 100 rounds to be even can be calculated as:

`W+L=100\\\\L=100-W\\\\\\Payoff=0=3*W-1*L=3W-1*(100-W)=3W+W-100\\\\0=4W-100\\\\W=25`

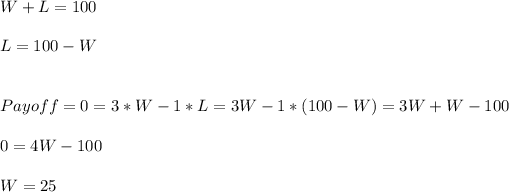
We have to win at least 25 rounds to have a positive payoff.

As the number of rounds is big, we will approximate the binomial distribution to a normal distribution with parameters:

`\mu=np=100*0.2=20\\\\\ \sigma=√(npq)=√(100*0.2*0.8)=4`

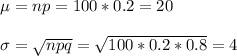
The z-value for x=25 is

`z=(X-\mu)/(\sigma)=(25-20)/(4)=1.25`

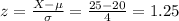
The probability of z>1.25 is

`P(X>25)=P(z>1.25)=0.10565`

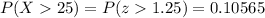
There is a 10.5% chance of having a positive payoff.

NOTE: if we do all the calculations for the binomial distribution, the chances of having a net payoff are 13.1%.