Question

Helium-oxygen mixtures are used by divers to avoid the bends and are used in medicine to treat some respiratory ailments. What percent (by moles) of He is present in a helium-oxygen mixture having a density of 0.538 g/L at 25 ∘C and 721 mmHg?

Answer 1

The percent by moles of helium in a helium-oxygen gas mixture at specific conditions can be calculated using the Ideal Gas Law and the density of the mixture, along with the molar masses of helium and oxygen to find the mole fraction of helium.

Step-by-step explanation:

To find the percent by moles of helium in the mixture, we can use the Ideal Gas Law equation PV = nRT, where P is the pressure, V is the volume, n is the number of moles, R is the Ideal Gas Constant, and T is the temperature in Kelvins. First, we need to convert the given conditions to the proper units: the pressure from mmHg to atm, and the temperature from degrees Celsius to Kelvins. Then, we can calculate the total moles of gas in the mixture.

Once we have the total moles, we can calculate the mole fraction of helium and oxygen by assuming a generic formula for the mixture (xHe + yO2), and keeping in mind that the density of the mixture is the mass of the gas divided by its volume. We have the density and the volume, so we can find the mass and then use the molar masses of helium and oxygen to find the ratio of moles for each gas. This ratio will give us the mole fraction of helium, from which we can easily calculate the percent by moles of He in the mixture.

Answer 2

Answer: The mole percentage of helium in the mixture is 64.75 %

Step-by-step explanation:

To calculate the molar mass of mixture, we use ideal gas equation, which is:

`PV=nRT`

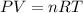
Or,

`P=(m)/(M)(RT)/(V)`

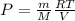
We know that:

`\text{Density}=\frac{\text{Mass}}{\text{Volume}}`

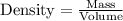
Rearranging the above equation:

`M=(dRT)/(P)`

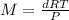
where,

M = molar mass of mixture = ?

d = density of mixture = 0.538 g/L

R = Gas constant =
`62.364\text{ L.mmHg }mol^(-1)K^(-1)`

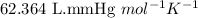
T = temperature of the mixture =
`25^oC=[25+273]K=298K`

P = pressure of the mixture = 721 mmHg

Putting values in above equation, we get:

`M=\frac{0.538g/L* 62.364\text{ L.mmHg }mol^(-1)K^(-1)* 298K}{721mmHg}\\\\M=13.87g/mol`

Molar mass of the mixture will be the sum of molar mass of each substance each multiplied by its mole fraction.

Let the mole fraction of Helium be 'x' and that of oxygen be '1-x'

`M=(x* M_(He))+((1-x)* M_(O_2))`

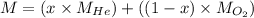
We know that:

Molar mass of helium = 4.00 g/mol

Molar mass of oxygen gas = 32g/mol

Putting values in above equation, we get:

`13.87=(x* 4)+((1-x)* 32)\\\\x=0.6475`

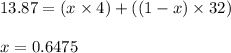
Mole fraction of helium in the mixture = 0.6475

Calculating the mole percentage of helium in the mixture:

`\text{Mole percentage of helium in the mixture}=x* 100\\\\\text{Mole percentage of helium in the mixture}=0.6475* 100=64.75\%`

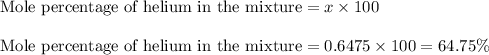
Hence, the mole percentage of helium in the mixture is 64.75 %