Answer:
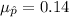 and
and

Explanation:
In sampling distribution of
 .
.
The mean and standard deviation of the sampling distribution of p is given by :-
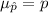
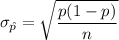 , where p= population proportion and n= sample size.
, where p= population proportion and n= sample size.
Let p be the population proportion of unmarried couples in the United States are mixed racially or ethnically.
As per given , we have
n = 100
p= 14% =0.14
Then, the mean and standard deviation of the sampling distribution of p will be :
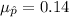

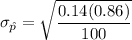
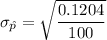
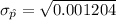
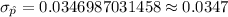
Hence, the required answer :
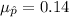 and
and
