Question

If the midpoint of segment AB is M(1,-3) and B(5,-10), find the coordinates of point A.

Answer 1

Therefore the required point A(x₁ , y₁) = A( -3 , 4 )

Explanation:

Given:

The midpoint of segment AB is M(1,-3)

and B(5,-10),

Let

point A( x₁ , y₁)

point B( x₂ , y₂) ≡ (5 , -10)

M(x , y) = (1 , -3 )

To Find:

point A( x₁ , y₁) = ?

Solution:

M is the midpoint of segment AB. {Given}

BY Mid point Formula we have

`M(x,y)=((x_(1)+x_(2) )/(2), (y_(1)+y_(2) )/(2))`

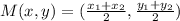
Substituting the given values in above equation we get

`M( 1, -3)=((x_(1)+5 )/(2), (y_(1)-10 )/(2))\\\\\textrm{on equating  the X coordinate and Y coordinate of M we get}\\1 =(x_(1)+5 )/(2)\\\\and\\-3=(y_(1)-10 )/(2)\\\\\therefore x_(1)+5=2\ and\ y_(1)-10 =-6\\\\\therefore x_(1) = 2-5=-3\ and\ y_(1)=10-6=4\\\\\therefore x_(1) = -3\ and \ y_(1)=4\\\\\therefore A(x_(1),y_(1))=A(-3,4)`

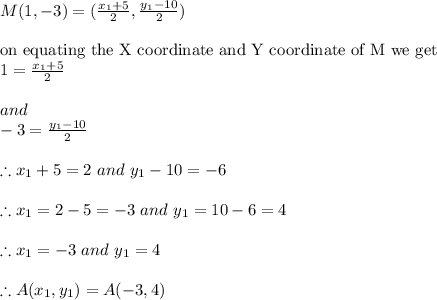
Therefore the required point A(x₁ , y₁) = A( -3 , 4 )