Answer:
0.2061,0.2182,0.7939,4
Explanation:
Given that a university found that in an introductory statistics course, about 40% of the enrolled students will pass the course with A or B grades, 30% will pass with a C and 10% will obtained D or F grades. 20% of the students withdraw without completing the course
i.e if X is the no of students withdrawing then X has a constant probability of 0.20 (since independent)
X is binomial with n =20
a) the probability that 2 or fewer will withdraw
=
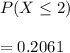
B. Compute the probability that exactly 4 will withdraw
=

C. Compute the probability that more than 3 will withdraw

D. Compute the expected number of students who will withdraw from the class.
=np = 20(0.2) = 4