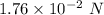Question

Approximate the skin friction drag on a 1m long by 60 cm diameter cylinder, located axially in a wind tunnel, when the air speed is 4.5 m/s. The pressure is atmospheric and the temperature is 50°C.

Answer 1

The drag force is
`1.76*10^(-2)\ N`

Step-by-step explanation:

Given that,

Diameter = 60 cm

Length = 1 m

Air speed = 4.5 m/s

Temperature = 50°C

We need to calculate the Reynolds number

Using formula of Reynolds number

`R_(e)=(vl)/(\mu)`

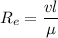
Put the value into the formula

`R_(e)=(4.5*1)/(1.900*10^(-5))`

`R_(e)=2.368*10^(5)`

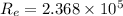
We need to calculate the drag coefficient

Using formula of drag coefficient

`C_(d)=\frac{2*0.646}{\sqrt{R_(e)}}`

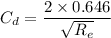
Put the value into the formula

`C_(d)=\frac{2*0.646}{\sqrt{2.368*10^(5)}}`

`C_(d)=0.002655`

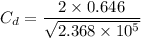
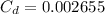
We need to calculate the drag force

Using formula of drag force

`F_(d)=(1)/(2)* C_(d)*\rho* A* v^2`

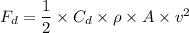
Put the value into the formula

`F_(d)=(1)/(2)*0.002655*1.095*0.6*1*(4.5)^2`

`F_(d)=0.01766\ N`

`F_(d)=1.76*10^(-2)\ N`

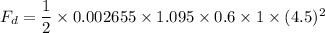
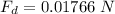
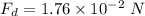
Hence, The drag force is
`1.76*10^(-2)\ N`