Answer:
Japan :
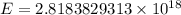
California :
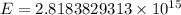
Explanation:
The magnitude of an earthquake on the Richter scale can be defined by

where E is the energy of the quake in joules.
Add 3.2 on both sides.
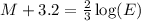
Multiply both sides by 3/2.
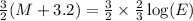
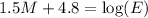
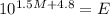
![[\because \log x=a\Rightarrow x=10^a]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/mdrs6qx3webln1wt5qiyhnbs4la6dl05s7.png)
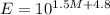 .... (1)
.... (1)
It is given that the 2011 Tohoku earthquake in Japan measured 9.1 on the Richter scale.
Substitute M=9.1 in equation (1).
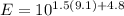
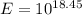
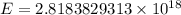
Therefore, the energy released by earthquake in japan is
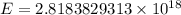 .
.
It is given that the 1999 Hector Mine earthquake in eastern California had a magnitude of 7.1.
Substitute M=7.1 in equation (1).
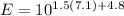
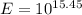
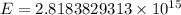
Therefore, the energy released by earthquake in California is
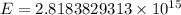 .
.