Question

At the moment a certain medicine is injected, its concentration in the bloodstream is 120120120 milligrams per liter. From that moment forward, the medicine's concentration drops by 30\%30%30, percent each hour.

Write a function that gives the medicine's concentration in milligrams per liter, C(t)C(t)C, left parenthesis, t, right parenthesis, ttt hours after the medicine was injected.

Answer 1

C(t)=120(0.7)^t

Explanation:

Answer 2

`C(t)=120(0.7)^t`

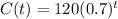
Explanation:

Let C(t) be the medicine's concentration in milligrams per liter, t hours after the medicine was injected.

It is given that the initial medicine's concentration is 120 milligrams per liter.

The medicine's concentration drops by 30% each hour.

The general exponential decay function is

`y=a(1-r)^t`

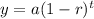
where, a is initial value, r is rate of change and t is time.

Substitute a=120, r=0.3 in the above equation.

`y=120(1-0.3)^t`

`y=120(0.7)^t`

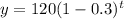
The function form of above equation is

`C(t)=120(0.7)^t`

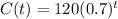
Therefore, the required function is
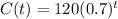`C(t)=120(0.7)^t`.