Question

There are premium tickets costing $99 each and rest are regualr tickets costing $25 each. A pile of 120 tickets have a total value of 5812. How many of each type ticket are in a piles

Answer 1

There are 38 premium tickets and 82 regular tickets in a pile.

Explanation:

Given,

Total number of tickets = 120

Total amount = $5812

Solution,

Let the number of premium tickets be x.

And the number of regular tickets be y.

Total number of tickets is the sum of total number of premium tickets and total number of regular tickets.

So the equation can be written as;

`x+y=120\ \ \ \ \ equation\ 1`

Again,total amount is the sum of total number of premium tickets multiplied by cost of each premium ticket and total number of regular tickets multiplied by cost of each regular ticket.

So the equation can be written as;

`99x+25y=5812\ \ \ \ equation\ 2`

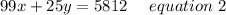
Now We will multiply equation 1 by 25 we get;

`x+y=120\\25(x+y)=120*25\\25x+25y= 3000 \ \ \ \ equation\ 3`

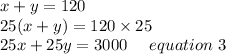
Now Subtracting equation 3 from equation 2 we get;

`(99x+25y)-(25x+25y)=5812-3000\\\\99x+25y-25x-25y=2812\\\\74x=2812\\\\x=(2812)/(74)=38`

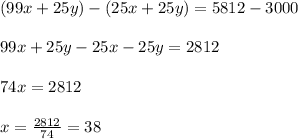
We will now substitute the value of x in equation 1 we get;

`x+y=120\\38+y=120\\y=120-38\\y=82`

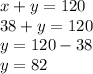
Hence There are 38 premium tickets and 82 regular tickets in a pile.