Question

The drawing shows three identical springs hanging from the ceiling. Nothing is attached to the first spring, whereas a 4.00-N block hangs from the second spring. A block of unknown weight hangs from the third spring. From the drawing, determine (a) the spring constant (in N/m) and (b) the weight of the block hanging from the third spring.

Answer 1

K = 26.667 N/m

Step-by-step explanation:

a) Using the newton's laws:

`W - F_k = 0`

Where W is the weigth of the block in the second spring and
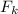`F_k` is the force of that spring. So:

W =
`F_k`

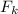
It means that:

W =
`Kx_2`

where K is the constant of the spring and x2 is the deformation of the second spring. Then, replacing values we get:

4N = K(0.15m)

Solving for K:

K = 26.667 N/m

b) At the same way, for the third spring, we have the equation:

W =
`Kx_3`

Where K is the same constant of the secor spring and x3 is the deformation of the third spring.

Finally, replacing values, we get:

W = (26.667N/m)(0.30)

W = 8N