Question

Can you help me find the test statistic AND Pvalue for a hypothesis test. The question is: In a survey respondents were asked would you be willing to pay higher taxes if the tax revenue went directly toward deficit reduction. Treat the respondents as a simple random sample of adults.

The survey results show


FEMALE MALE


Yes 33 30

No 65 72

Total 98 102

Answer 1

Test statistic z=0.65

P-value=0.52

Fail to reject the null hypothesis.

Explanation:

Here we have to perform a hypothesis test on the difference of proportions. We may want to answer if there is significant difference in the proportions of male and females.

The null and alternative hypothesis are:

`H_0: \pi_1=\pi_2\\\\H_1: \pi_1\\eq\pi_2`

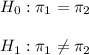
The significance level is defined as 0.05.

The YES proportion for females is:

`p_1=33/98=0.337`

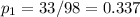
The YES proportion for males is:

`p_2=30/102=0.294`

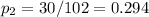
The weighted average of p can be calculated as:

`p=(n_1*p_1+n_2*p_2)/(n_1+n_2)=(33+30)/(98+102)=0.315`

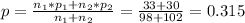
With this p, we estimate the standard deviation

`s=\sqrt{(p(1-p))/(n_1)+(p(1-p))/(n_2) }=\sqrt{(0.315(1-0.315))/(98)+(0.315(1-0.315))/(102) }=0.066`

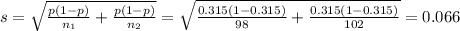
The test statistic z can be calculated as:

`z=(p_1-p_2)/(s) =(0.337-0.294)/(0.066)=(0.043)/(0.066)=0.65`

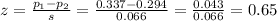
We can calculate the p-value for z, taking into account is a two-sided test

`P(|z|>0.65)=0.52`

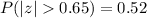
The P-value (0.52) is greater than the significance level (0.05), so the effect is not significant. It failed to reject the null hypothesis.

We have enough evidence to conclude that the proportions that vote YES are different between genres.