Question

The data below represent the number of days​ absent, x, and the final​ grade, y, for a sample of college students at a large university. Complete parts​ (a) through​ (e) below. No. of​ absences, x 0 1 2 3 4 5 6 7 8 9 Final​ grade, y 88.5 85.7 82.8 80.3 77.4 73.1 63.6 68.1 65.2 62.4 ​(a) Find the​ least-squares regression line treating the number of​ absences, x, as the explanatory variable and the final​ grade, y, as the response variable.

Answer 1

The equation of the regression line is:
`y~=~88.518 ~-~ 3.068 \cdot x`

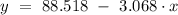
Explanation:

Linear regression is a linear approach to modelling the relationship between a dependent variable and one or more independent variables.

Let X be the independent variable and Y be the dependent variable. We will define a linear relationship between these two variables as follows:

`Y=bX+a`

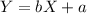
We have the the following data:

To find the line of best fit for the points, follow these steps:

Step 1: Find
`X\cdot Y` and
`X\cdot X` as it was done in the table.

Step 2: Find the sum of every column:

`\sum{X} = 45 ~,~ \sum{Y} = 747.1 ~,~ \sum{X \cdot Y} = 3108.8 ~,~ \sum{X^2} = 285`

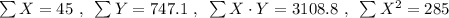
Step 3: Use the following equations to find intercept a and slope b:

`\begin{aligned}        a &= \frac{\sum{Y} \cdot \sum{X^2} - \sum{X} \cdot \sum{XY} }{n \cdot \sum{X^2} - \left(\sum{X}\right)^2} =             ( 747.1 \cdot 285 - 45 \cdot 3108.8)/( 10 \cdot 285 - 45^2) \approx 88.518 \\ \\b &= \frac{ n \cdot \sum{XY} - \sum{X} \cdot \sum{Y}}{n \cdot \sum{X^2} - \left(\sum{X}\right)^2}        = ( 10 \cdot 3108.8 - 45 \cdot 747.1 )/( 10 \cdot 285 - \left( 45 \right)^2) \approx -3.068\end{aligned}`

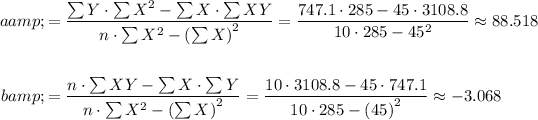
Step 4: Assemble the equation of a line

`\begin{aligned} y~&=~a ~+~ b \cdot x \\y~&=~88.518 ~-~ 3.068 \cdot x\end{aligned}`

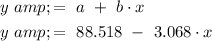
The graph of the regression line is: