Question

A company makes two different sized ice cream cones the smaller cone are 3.5 inches tall and have a diameter of 3 inches the larger cones are 5.1 inches tall and have a diameter of 4.5 inches

Answer 1

Question:

A company makes two different-sized ice cream cones. The smaller cones are 3.5 inches tall and have a diameter of 3 inches. The larger cones are 5.1 inches tall and have a diameter of 4.5 inches. Abour how much greater, to the nearest tenth of a cubic inch, is the volume of the larger cone than the volume of the smaller cone?

Answer:

The volume of the larger cone is 19
`inches^3` greater than the volume of the smaller cone

Explanation:

Given:

Length of small cone = 3.5 inches

Diameter of small cone = 3 inches

Length of large cone = 5.1 inches

Diameter of large cone = 4.5 inches

To Find :

how much greater is the volume of the larger cone than the volume of the smaller cone = ?

Solution:

Step 1 : Finding the volume of small cone

Radius =
`(3)/(2)` = 1.5 inches

Volume of the cone =
`(1)/(3) \pi r^2 h`

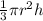
Substituting the values

Volume of smallcone =
`(1)/(3) \pi * (1.5)^2 (3.5)`

=>
`(1)/(3) \pi * (2.25)(3.5)`

=>
`(1)/(3) \pi * (7.875)`

=>
`(1)/(3) * 24.7275`

=>
`(24.7275)/(3)`

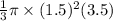
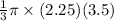
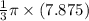
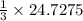
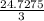
=>8.2425

Step 2 : Finding the volume of large cone

Radius =
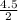`(4.5)/(2)` = 2.25 inches

Volume of the cone =
`(4.5)/(2)`

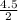
Substituting the values

Volume of largecone =
`(1)/(3) \pi * (2.25)^2 (5.1)`

=>
`frac{1}{3} \pi * (5.0625)(5.1)`

=>
`(1)/(3) \pi * (21 .818)`

=>
`(1)/(3) * (81.070)`

=>
`(81.070)/(3)`

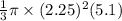
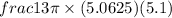
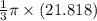
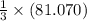
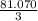
=>27.02

Volume of large cone - volume of small cone

=>27.02 - 8.2425

=>18.77

=>19(rounding off to nearest tenth)