Question

Kailee paid $14.84 for stamps. The number of .49-cents stamps was four less then three times the number of 21-cent stamps. How many 49-cent stamps and how many 21-cent stamps did kailee buy?

Answer 1

Kailee bought 26 of 49-cents stamps and 10 of 21-cents stamps.

Explanation:

Given:

Total Money paid for stamps = $14.84

Let the number of 49-cents stamps be x.

Also Let the number of 21-cents stamps be y.

Now Total Money paid is equal to sum of number of 49-cents stamps and number of 21-cents stamps.

100 cents = 1$

So 49 cents = $0.49

and 21 cents = $0.21

Hence equation be framed as;

`0.49x+0.21y =14.84 \ \ \ \ equation \ 1`

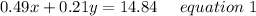
Also Given:

number of .49-cents stamps was four less then three times the number of 21-cent stamps.

hence we can say that;

`x=3y-4\ \ \ \ equation \ 2`

Now Substituting the value of equation 2 in equation 1 we get;

`0.49(3y-4)+0.21y=14.84\\1.47y- 1.96+0.21y=14.84\\1.68y=14.84+1.96\\1.68y = 16.8\\y=(16.8)/(1.68)=10`

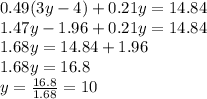
Now substituting the value of y in equation 2 we get;

`x=3y-4\\x=3*10-4\\x=30-4\\x=26\\`

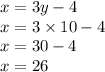
Hence Kailee bought 26 of 49-cents stamps and 10 of 21-cents stamps.