Question

Computech Corporation is expanding rapidly and currently needs to retain all of its earnings; hence, it does not pay dividends. However, investors expect Computech to begin paying dividends, beginning with a dividend of $0.50 coming 3 years from today. The dividend should grow rapidly—at a rate of 35% per year—during Years 4 and 5, but after Year 5, growth should be a constant 7% per year. If the required return on Computech is 13%, what is the value of the stock today?

Answer 1

$10.08

Step-by-step explanation:

First, find dividend per year;

D3 = 0.50

D4 = 0.50(1.35) = 0.675

D5 = 0.675 (1.35 ) = 0.9113

D6 = 0.9113 (1.07) = 0.9751

Next, find the present value of each dividend at 13% rate;

PV (of D3) = 0.50/(1.13^3) = 0.3465

PV (of D4) = 0.675/(1.13^4) = 0.4140

PV (of D5) = 0.9113/(1.13^5) = 0.4946

`PV (of D6) = ((0.9751)/(0.13-0.07) )/(1.13^(5) ) \\ \\ = (16.2517)/(1.8424)`

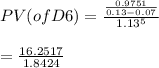
PV (of D6 )= 8.8209

Add the PVs to find the stock price;

= 0.3465 + 0.4140 + 0.4946 + 8.8209

= $10.08