Answer:
b.

Explanation:
Notation
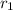 represent the number of successes for the event 1
represent the number of successes for the event 1
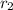 represent the number of successes for the event 2
represent the number of successes for the event 2
 represent the sample for the event 1
represent the sample for the event 1
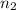 represent the sample for the event 2
represent the sample for the event 2
Concepts and formulas to use
We need to conduct a hypothesis in order to test if two proportions are equal, the system of hypothesis are:
Null hypothesis:

Alternative hypothesis:
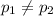
When we conduct a proportion test we need to use the z statistic, and the is given by:
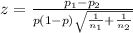 (1)
(1)
The Two Sample Proportion Test is used to assess whether a population proportion
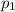 is significantly (different, higher or less) from another proportion value
is significantly (different, higher or less) from another proportion value
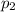 .
.
The best estimate to the polled estimate for p is given by:
