Answer: +2.10V
Step-by-step explanation:
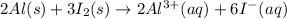
Using Nernst equation :
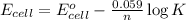
![E_(cell)=E^o_(cell)-(0.059)/(n)\log [Al^(3+)]^2* [I^-]^6](https://img.qammunity.org/2020/formulas/physics/college/n6ymsp7znyje34rn30r93bqiwfj9olkni4.png)
where,
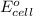 = standard emf for the cell = +2.20 V
= standard emf for the cell = +2.20 V
n = number of electrons in oxidation-reduction reaction = 6
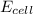 = emf of the cell = ?
= emf of the cell = ?
![[Al^(3+)]](https://img.qammunity.org/2020/formulas/chemistry/college/7alerx4hp12zkqu9rvclpa6xcpb2kmxn98.png) = concentration =
= concentration =
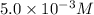
![[I}^(-)]](https://img.qammunity.org/2020/formulas/physics/college/5ngsig5kr7saho6mmimb03p1j7z9qprrf1.png) = concentration =
= concentration =
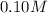
Now put all the given values in the above equation, we get:
![E_(cell)=+2.20-(0.059)/(6)\log [5.0* 10^(-3)]^2* [0.10]^6](https://img.qammunity.org/2020/formulas/physics/college/5u3svmmadkwsm1puynqzwmkd47yt91dx85.png)
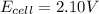
The standard emf for the cell using the overall cell reaction below is +2.10 V